A number of recent articles have explored the relationship between temperature and R-value with an emphasis on the apparent reduction in R-value demonstrated by polyisocyanurate (or polyiso) roof insulation at cold temperatures. The science behind this apparent R-value decrease is relatively simple: All polyiso foam contains a blowing agent, which is a major component of the insulation performance provided by the polyiso foam. As temperatures decrease, all blowing agents will start to condense, and at some point this will result in a marginally reduced R-value. The point at which this occurs will vary to some extent for different polyiso foam products.
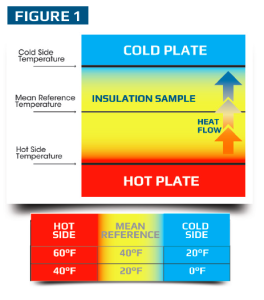
A mean reference temperature of 40 F is based on the average between a hot-side temperature of 60 F and a cold-side temperature of 20 F.
TO DETERMINE the appropriate temperature for R-value testing of polyiso, it is important to review how R-value is tested and measured. Figure 1 provides a simplified illustration of a “hot box” apparatus used to test and measure the R-value of almost all thermal-insulating materials. The insulation sample is placed within the box, and a temperature differential is maintained on opposing sides of the box. To generate accurate R-value information, the temperature differential between the opposing sides of the box must be relatively large—typically no less than 40 F according to current ASTM standards. The results of this type of test are then reported based on the average between these two temperature extremes, which is referred to as mean reference temperature. As shown in Figure 1, a mean reference temperature of 40 F is based on the average between a hot-side temperature of 60 F and a cold-side temperature of 20 F. In a similar manner, a mean reference temperature of 20 F is based on a hot-side temperature of 40 F and a cold-side temperature of 0 F.
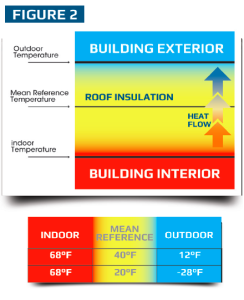
NOW THAT we’ve had an opportunity to discuss the details of R-value testing, let’s apply the principles of the laboratory to the real-world situation of an actual building. Just like our laboratory hot box, buildings also have warm and cold sides. In cold climates, the warm side is located on the interior and the cold side is located on the exterior. If we assume that the interior is being heated to 68 F during the winter, what outdoor temperature will be required to obtain a mean reference temperature of 40 F or 20 F? Figure 2 provides a schematic analysis of the appropriate mean reference temperature.
As illustrated in Figure 2, the necessary outdoor temperature needed to attain a 40 F mean reference temperature would be 12 F while an outdoor temperature as low as -28 F would be needed to obtain a 20 F mean reference temperature. And herein lies a glaring problem with many of the articles published so far about the relationship between temperature and R-value. Although a 20 F or 40 F “reference temperature” may sound reasonable for measuring R-value, average real-world conditions required to obtain this reference temperature are only available in the most extreme cold climates in the world. With the exception of the northernmost parts of Canada and the Arctic, few locations experience an average winter temperature lower than 20 F.
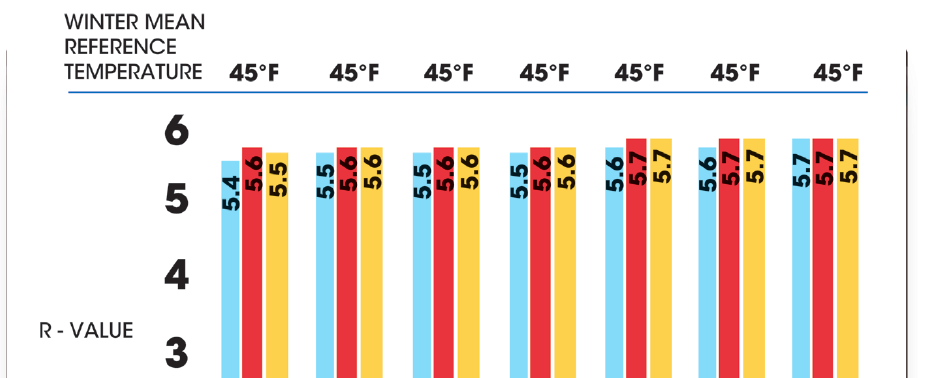
To help illustrate the reality of average winter temperature in North America, a recent white paper published by the Bethesda, Md.-based Polyisocyanurate Insulation Manufacturers Association (PIMA), “Thermal Resistance and Temperature: A Report for Building Design Professionals”, which is available at Polyiso.org, identifies these average winter temperatures by climate zone using information from NOAA Historical Climatology studies. As shown in Table 1, page 2, the PIMA white paper identifies that actual average winter temperature varies from a low of 22 F in the coldest North American climate zone (ASHRAE Zone 7) to a high of 71 F in the warmest climate zone (ASHRAE Zone 1).
In addition to identifying a realistic winter outdoor average temperature for all major North American climate zones, Table 1 also identifies the appropriate mean reference temperature for each zone when a 68 F indoor design temperature is assumed. Rather than being as low as 40 F or even 20 F as sometimes inferred in previous articles, this mean winter reference temperature varies from a low of no less than 45 F in the coldest climate zone to above 50 F in the middle climate zones in North America.



If you were selling smoke and mirror’s your inventory would be completely sold out. This article was obviously written by the PIMA just to protect its member’s. Using mean temperatures does not work with a material that does not have thermal conductivity curve that is linear. I would have assumed the Association representing the polyisocyanurate industry would have known this. Using data from this article would be unwise as it does not represent any real life scenarios where polyisocyanurate insulation would be installed. Using temperature dependant thermal conductivities as indicated by NRCA or BSC would be a more realistic approach for designer to use to calculate effect heat loss, if the data above was used it could severely over predict the effectiveness of the assembly. This over prediction can potentially lead to condensation issues as well as higher energy bills.